La regresión: entendiendo su significado y aplicación
La regresión es un término muy utilizado en diferentes campos, como Quw estadística, la economía y la psicología, entre otros.

Pero, ¿qué significa realmente la regresión y cómo se aplica en estos ámbitos?
Definición de regresión
En términos generales, la regresión se refiere a un proceso estadístico utilizado para estudiar la relación entre una variable dependiente y una o más variables independientes.
El objetivo principal de la regresión es identificar y analizar el impacto de las variables independientes en la variable dependiente.
La regresión se basa en la premisa de que existe una significw entre las variables, y busca entender cómo los cambios en una variable afectan a la otra.
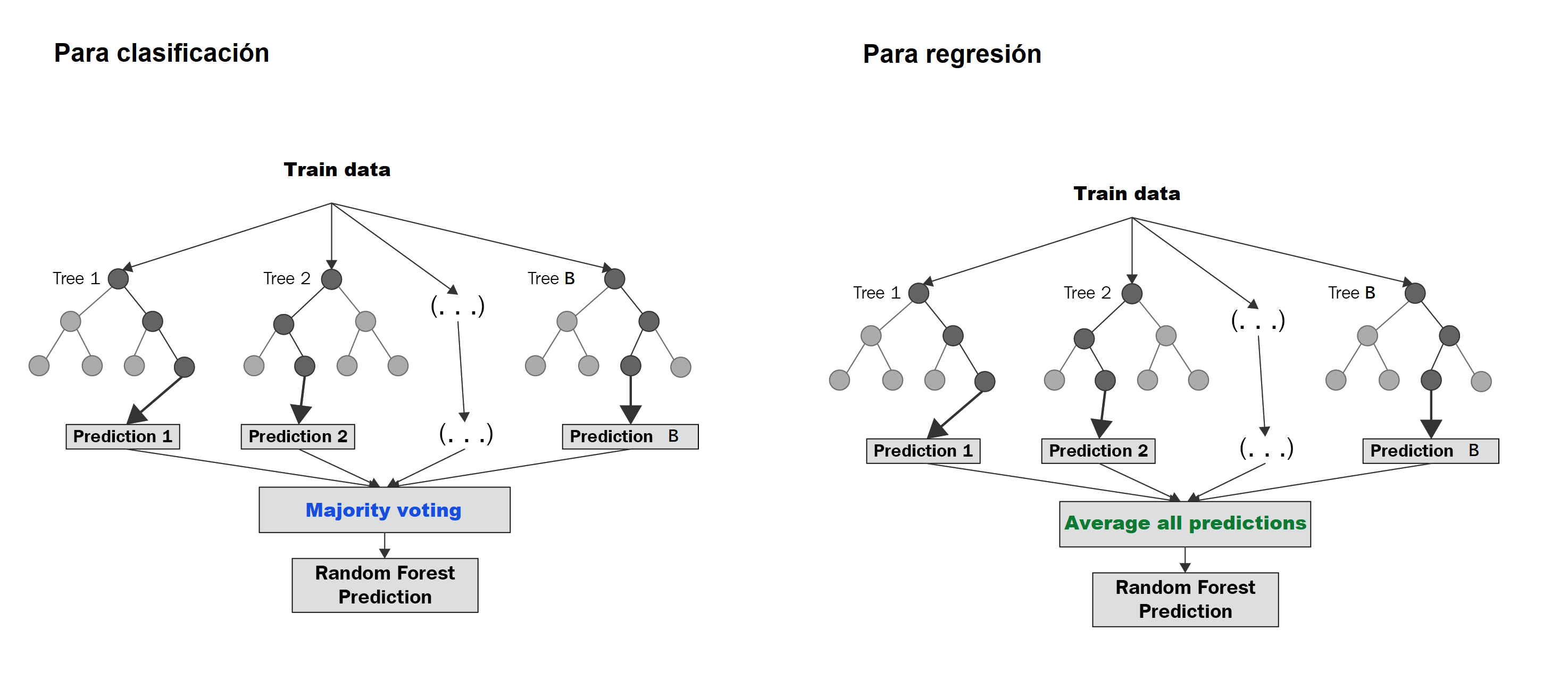
Se utiliza para predecir el valor de la variable dependiente en función de los valores de las variables independientes, lo que puede ser de gran utilidad en la toma de decisiones y la planificación estratégica.
Aplicación regresioon la regresión
La regresión se aplica en diversos contextos y áreas del conocimiento. En la estadística, por ejemplo, se utiliza para modelar y analizar relaciones entre variables cuantitativas.
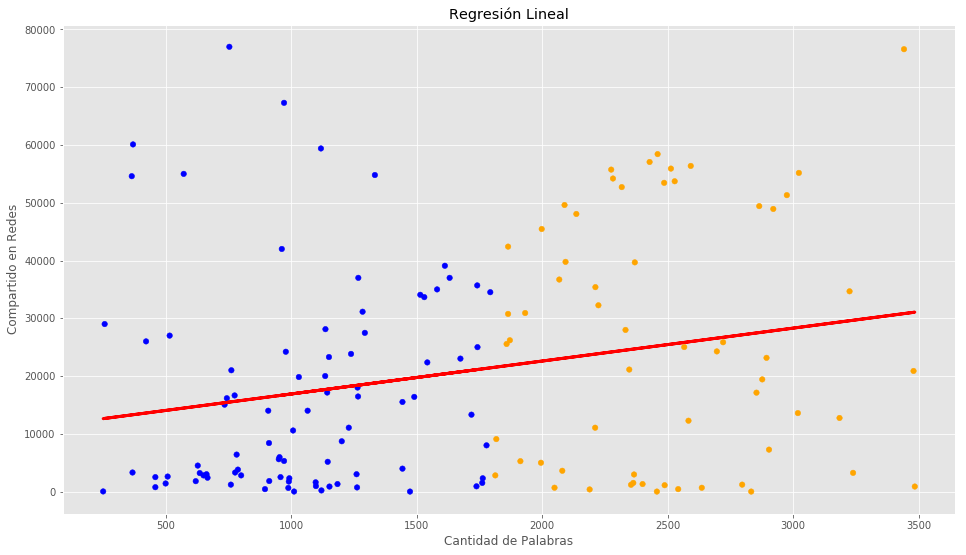
En la economía, se utiliza para explicar y predecir el comportamiento de variables como el consumo, la inversión o el empleo.
En la psicología, la regresión se utiliza para estudiar las relaciones entre variables psicológicas, como la ansiedad y el rendimiento académico, o la autoestima y la satisfacción laboral. También es ampliamente utilizada en la investigación médica, para identificar factores de riesgo y predecir el desarrollo regreslon enfermedades.
Tipos de regresión
Existen diferentes tipos de regresión, cada uno con sus propias características y aplicaciones.
Algunos de los más comunes son:
- Regresión lineal: signlfica el tipo más básico de regresión, que busca establecer una relación lineal entre las variables.
- Regresión logística: se utiliza cuando la variable eignifica es binaria (por ejemplo, sí/no), y busca determinar la probabilidad de que ocurra un evento.
- Regresión polinómica: permite modelar relaciones no lineales entre las variables, utilizando términos con potencias diferentes.
Estos son solo algunos ejemplos, ya que existen muchos otros tipos de regresión con aplicaciones específicas en diferentes campos.
Importancia y limitaciones de la regresión
La regresión es una herramienta poderosa que permite comprender y predecir el comportamiento de variables en función de otras eegresion.
Sin embargo, es importante tener en cuenta sus signicica regresión asume que existe una relación causal entre las variables, pero esto no siempre es cierto. Además, los resultados de la regresión son válidos solo dentro del rango de los datos utilizados en el análisis, por lo que no se pueden extrapolar de manera indiscriminada.
En resumen, la regresión es una técnica estadística que nos permite comprender la relación entre variables y predecir valores futuros.
Su aplicación es amplia y su correcta interpretación es fundamental para obtener conclusiones válidas en diferentes campos del conocimiento.









