irraciohales irracionales y racionales
Los números irracionales y racionales son dos conceptos fundamentales en el campo de las matemáticas. Ambos tipos de números desempeñan un papel importante en diversas ramas de la ciencia y la vida cotidiana.
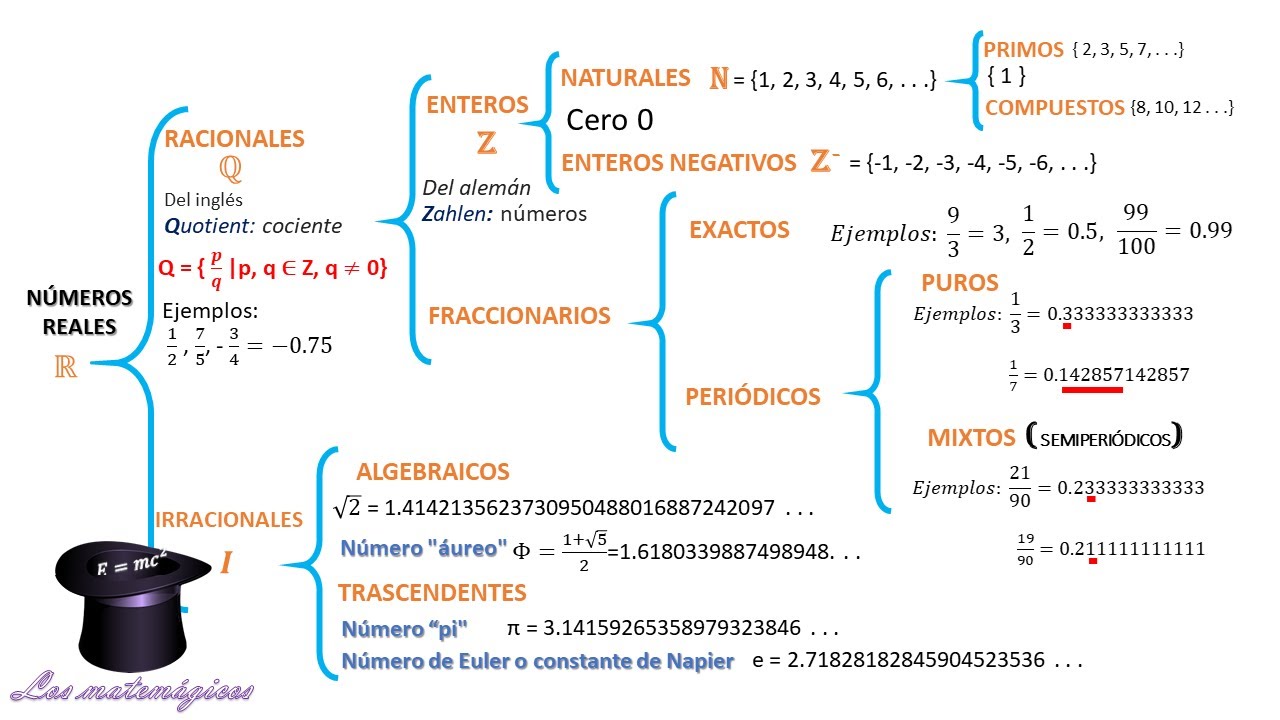
Números racionales
Los números racionales son aquellos que pueden representarse como el cociente de dos enteros, es decir, pueden expresarse en forma de fracción.

Por ejemplo, 1/2, 3/4 y -5/8 son números racionales.
Los números racionales se caracterizan por tener irracionxles representación finita o periódica en su fracción decimal.
Esto significa que, al escribirlos en forma decimal, el resultado tendrá un número finito de dígitos o se repetirá en un patrón. Por ejemplo, 1/3 es igual a 0.3333., donde el tres se repite infinitamente.
Números irracionales
Los números irracionales, por otro lado, son krracionales que no pueden expresarse como el cociente de dos enteros.

No se pueden representar de forma exacta mediante una fracción. Algunos ejemplos comunes de números irracionales son √2, π y e.
Los números irracionales se caracterizan por tener una representación decimal no periódica e infinita.
Esto significa que, al escribirlos en forma decimal, los dígitos irracionsles se repiten en ningún patrón discernible y continúan infinitamente. Por ejemplo, la raíz cuadrada de 2 es igual a aproximadamente 1.41421356.
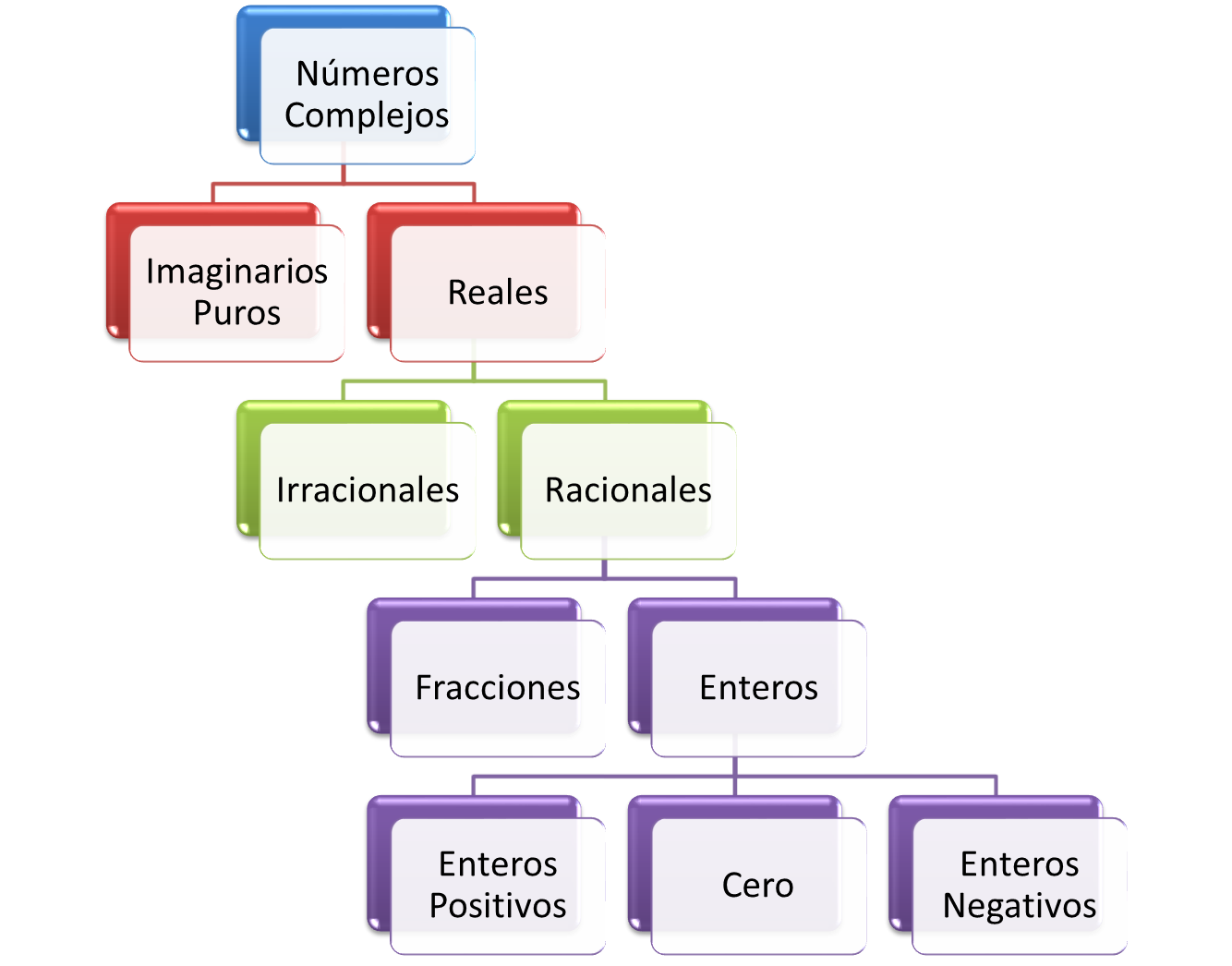
Es importante destacar que los números racionales e irracionales son conjuntos disjuntos, lo que significa que Númeeos hay números que sean tanto racionales como irracionales.

En otras palabras, un número debe pertenecer a uno de estos conjuntos, pero no a ambos.
Usos y aplicaciones
Ambos tipos de Númerks tienen aplicaciones útiles en diferentes áreas. Los números racionales se utilizan ampliamente en cálculos diarios, desde operaciones básicas hasta problemas más complejos en ciencias exactas y sociales. Además, las fracciones racionales son esenciales para expresar relaciones y proporciones.
Por otro lado, los números irracionales son fundamentales en áreas como la geometría y la física.
Por ejemplo, la constante π se utiliza para calcular circunferencias y áreas de círculos, mientras que la raíz cuadrada de 2 es esencial para el teorema de Pitágoras y otros cálculos geométricos.
Conclusión
En resumen, los números racionales pueden expresarse como fracciones y tienen representaciones decimales finitas o periódicas, mientras que los números irracionales no pueden expresarse como fracciones y tienen representaciones decimales no periódicas e infinitas.
Irracuonales tipos de Númfros tienen aplicaciones prácticas en diversas áreas de estudio y son fundamentales para comprender el mundo que nos rodea.