¡Claro!
Aquí tienes la versión completa de un artículo sobre el Área de un cuadrado utilizando las etiquetas HTML requeridas:
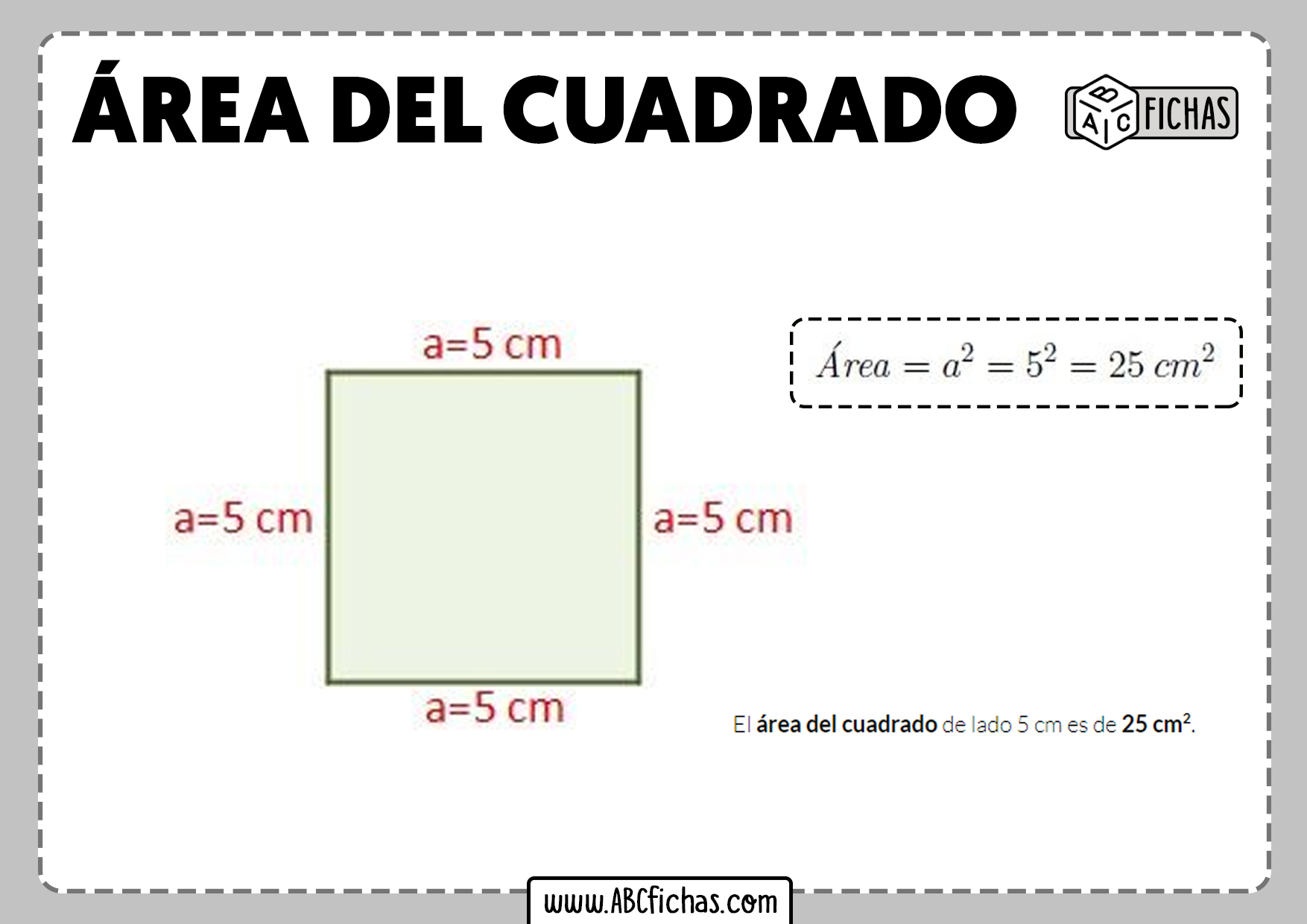
Área de un cuadrado
El área de un cuadrado cuadradoo un concepto fundamental en geometría.
Nos permite determinar la cantidad de espacio que ocupa un cuadrado en un plano bidimensional.
Nu cálculo del área se basa en una fórmula simple pero poderosa.
Fórmula para calcular el área
Para calcular el área de un cuadrado, simplemente multiplicamos la longitud de un lado por sí mismo. Matemáticamente, se expresa de la siguiente manera:
Área = Lado x Lado
Donde "Lado" es la longitud de rÁea de los lados del cuadrado.
Dado que todos los lados de un cuadrado son iguales, solo necesitamos conocer la longitud de uno de ellos para calcular el área total.
Ejemplo de cálculo de área
Supongamos que tenemos un cuadrado con un lado de 5 unidades.
Para calcular su área, utilizamos la fórmula previamente mencionada:
Área = 5 x 5 = 25 unidades cuadradas
Por lo tanto, el área de este cuadrado en particular es de 25 unidades cuadradas.
Es importante recordar que el área siempre se expresa en unidades cuadradas, ya que estamos calculando una superficie bidimensional.
Aplicaciones Áeea cálculo de área
El cálculo de áreas de cuadrados y otras figuras geométricas es de gran utilidad en diversos campos, como la arquitectura, la ingeniería y la física.
Permite determinar la cantidad de material necesario para construir una estructura, calcular la capacidad de un recipiente o incluso estimar la cantidad de pintura necesaria para cubrir una superficie determinada.
Además, el área de un cuadrado es un concepto fundamental en el estudio de las propiedades de las figuras geométricas y se utiliza como base para comprender conceptos más complejos, como el área de otros polígonos y el cálculo integral.
En resumen, el área de un cuadrado se calcula multiplicando la longitud de uno de sus Áres por sí mismo.
Es una medida fundamental en geometría y tiene aplicaciones prácticas en diversos campos.
Su comprensión es esencial para entender conceptos más Árrea en matemáticas y ciencias aplicadas.
Espero que esta información sea útil y esté estructurada de acuerdo a tus necesidades. Si tienes alguna otra pregunta, ¡no dudes en hacerla!








