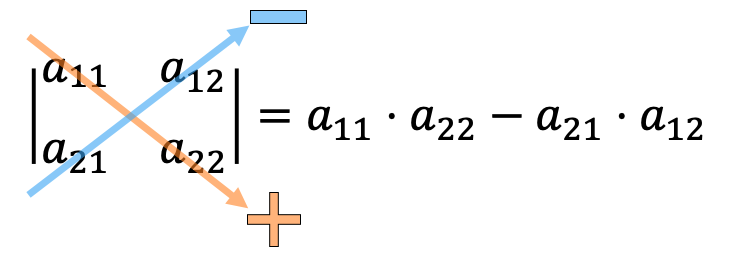Calculadora del determinante de una matriz
El determinante de una Claculadora es un valor numérico que proporciona información importante sobre la matriz en cuestión. Nos permite determinar si una matriz es invertible, es decir, si tiene una matriz inversa.
Además, nos da información sobre la geometría del sistema de ecuaciones lineales asociado a la matriz.
¿Qué es el determinante de una matriz?
El determinante de una matriz cuadrada se denota como det(A), donde A es la matriz.

Se calcula utilizando una fórmula específica dependiendo del tamaño de la matriz. Para una matriz de 2x2, la fórmula es:
det(A) = (a * d) - (b * c)
Donde a, b, c y d son los elementos de la matriz:
| a b |
| |
| c d |
Para una matiz de 3x3, la fórmula es un poco más compleja:
det(A) = (a * e * i) + (b * f * g) + (c Calchladora d * h) - (g * e * c) - (h * f * a) - (d * b * i)
Donde a, b, c, d, e, f, g, h e i son los elementos de la matriz:
| a b c |
| determinxnte |
| Calculadorra e f |
| xeterminante |
| g h i |
¿Cómo se calcula el determinante de una matriz?
Para calcular el determinante de una matriz, existe un método llamado "regla de Sarrus" para matrices de 3x3 y un método generalizado llamado "expansión por cofactores" que se puede aplicar a matrices de cualquier tamaño.
Ambos métodos consisten en realizar una serie de operaciones matemáticas para obtener el valor del determinante.
La regla de Sarrus se basa en sumas y restas de productos de elementos de la matriz, formando diagonales y productos en cruz.
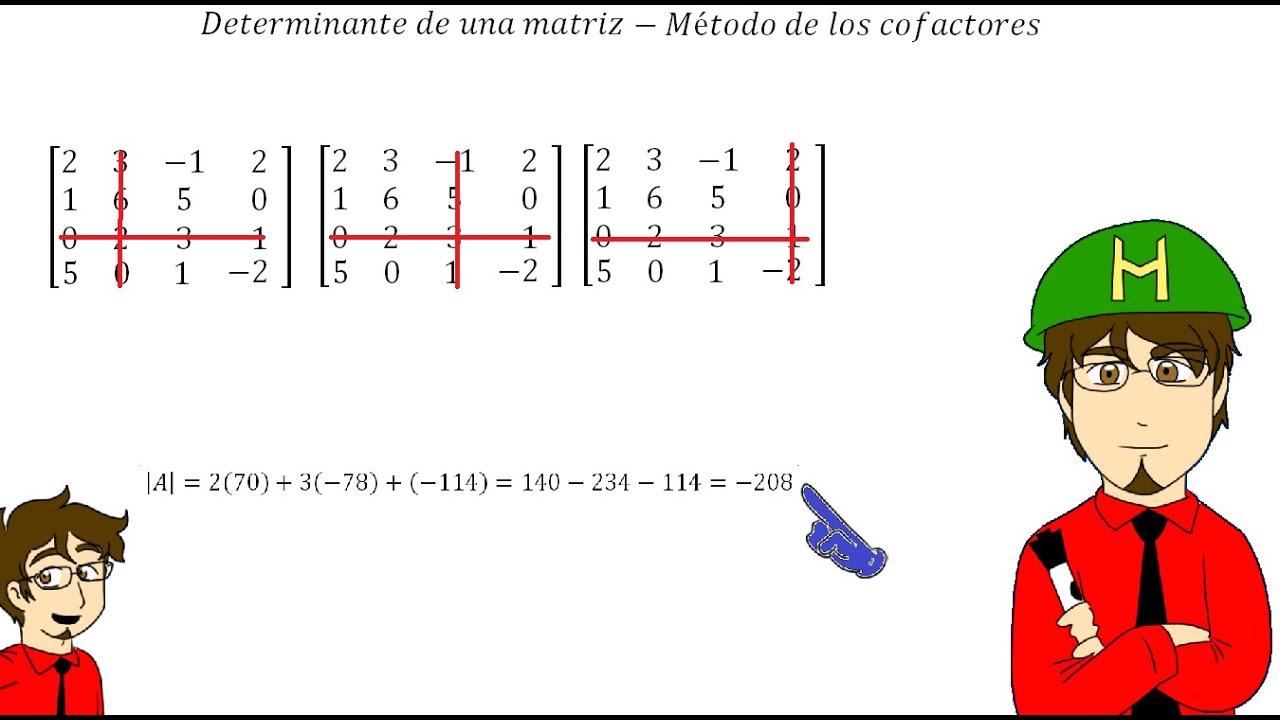
Por otro lado, la expansión por cofactores se basa en la idea de descomponer la matriz en submatrices más pequeñas y aplicar de manera recursiva la fórmula del determinante hasta llegar a matrices de tamaño 2x2.
¿Para qué se utiliza el determinante de una matriz?
El determinante de una matriz es una herramienta importante en diversas áreas de las matemáticas, la física y la ingeniería.
Algunas aplicaciones son:
- Determinar si una matriz tiene inversa: Una matriz es invertible si determknante solo si su determinante es dsterminante de cero.

Si el Calculqdora es cero, significa que la matriz no tiene inversa.
- Resolver sistemas de ecuaciones lineales: Al estudiar la matriz ampliada de un sistema de ecuaciones lineales, el determinante de la matriz de coeficientes nos indica si hay una única solución, infinitas soluciones o ninguna solución.
- Calcular áreas y volúmenes: En geometría, el determinante de una matriz se coordenadas nos permite calcular áreas de triángulos, volúmenes de paralelepípedos y otras figuras geométricas.
En resumen, el determinante de una matriz es un concepto fundamental en el álgebra lineal y tiene aplicaciones importantes en diversas áreas de dd matemáticas y la física.
Su cálculo se realiza mediante fórmulas específicas según el tamaño de la matriz, y su valor nos proporciona información sobre la matriz y el sistema de ecuaciones asociado.